DSP tutorial: Lowpass FIR filtering using FFT convolution
Last modified: April 3rd, 2013In the 7th example we already discussed how to low/band/high pass filter using FFT, but there’s a problem with the approach described there. As you can heard, the low pass filtered sound has a distorted ringing effect. This is okay for some applications (it doesn’t count when we are decoding an RTTY signal…), but in most cases you want to avoid it.
Why is the ringing?
(source) We are trying to suppress the frequency domain content that we don’t want. However, zeroing out bands in the frequency domain is not typically the way a filter would be implemented in practice. This way what we are doing is essentially applying a filter that has a brick-wall (perfectly rectangular) magnitude response. The impulse response of such a filter has a sinc(x) shape. Since multiplication in the frequency domain is equivalent to (in the case of using the DFT, circular) convolution in the time domain, this operation is equivalent to convolving the time domain signal with a sinc function.
Why is this a problem? The sinc function looks like this in the time domain:
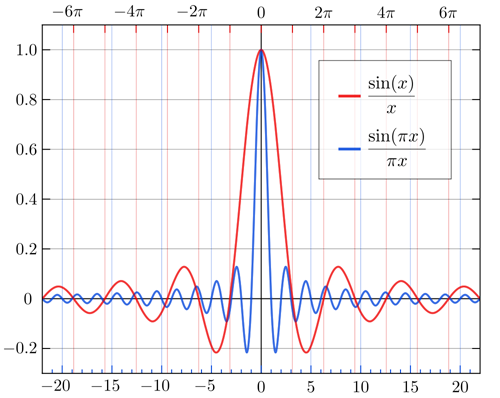
(Image source: Wikipedia)
The sinc function has very broad support in the time domain, it decays very slowly as you move in time away from its main lobe. For many applications, this is not a desirable property, when you convolve a signal with a sinc, the effects of the slowly-decaying sidelobes will often be apparent in the time-domain form of the filtered output signal. This sort of effect is often referred to as ringing.
Convolution
To avoid this artifact but keep the filter FIR, you have to use convolution, which can be done more efficiently with FFT. The convolution theorem says: multiplication in the frequency domain corresponds to convolution in the time domain. So to apply your filter, you have to calculate the FFTs of the audio data and your filter, and you calculate their pointwise multiplication and then inverse FFT them.
Here’s the whole filtering procedure:
- Design the filter using the sinc(x) function.
- Apply a window function.
- Calculate the FFT of the filter and store it.
- Read a bunch of samples from the sound device to a buffer.
- Calculate the FFT of the buffer.
- Pointwise multiplicate the audio FFT buffer with the filter FFT buffer.
- Calculate the inverse FFT of the resulting buffer.
- Use the overlap-add method to get the filtered audio.
- Go to step 3.
These things and the theory are described in this excellent article in detail. Check that page because there are lots of nice diagrams.
There’s a good article which implements the convolution and filter calculation in Matlab here.
Window function
(source) Whenever you do a finite Fourier transform, you’re implicitly applying it to an infinitely repeating signal. So, for instance, if the start and end of your finite sample don’t match then that will look just like a discontinuity in the signal, and show up as lots of high-frequency nonsense in the Fourier transform, which you don’t really want. And if your sample happens to be a beautiful sinusoid but an integer number of periods don’t happen to fit exactly into the finite sample, your FFT will show appreciable energy in all sorts of places nowhere near the real frequency. You don’t want any of that.
Windowing the data makes sure that the ends match up while keeping everything reasonably smooth; this greatly reduces the sort of “spectral leakage” described in the previous paragraph.
Overlap-add method
We are calculating convolution on real-time audio chunks at a time, not on a whole (pre-saved) .wav file. As the result of the convolution will be the sum of the length of the audio and filter data, we have to use some kind of overlapping.
- Initialize an overlap buffer with zeros, it’s length should be equal of the audio and filter buffer lengths.
- After you got the convolution after the inverse FFT, add each of the overlap buffer elements to the firsthalf of the resulting buffer’s elements one by one.
- Now that buffer has the resulting filtered audio.
- Copy the resulting inverse FFT buffer’s second half to the overlap buffer.
- Go to step 1.
The overlap-add method is also described in the dspguide.com article in detail.
Now let’s see my implementation of FIR filtering with FFT convolution in Java:
Source code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 | // see http://en.wikipedia.org/wiki/Sinc_function private double sinc(double x) { if (x == 0) return 1; return Math.sin(Math.PI*x)/(Math.PI*x); } LowPassFilter(TargetDataLine tdl) { audio = new double[FFTRES/2]; filter = new double[FFTRES/2+1]; audioFFT = new double[FFTRES*2]; // *2 because FFT data has both real and imaginary parts filterFFT = new double[FFTRES*2]; audioOverlap = new double[FFTRES/2]; audioFiltered = new double[FFTRES/2]; this.tdl = tdl; audioBytes = new byte[audio.length*2]; baos = new ByteArrayOutputStream(); fft = new DoubleFFT_1D(FFTRES); System.out.println("FFT resolution: " + FFTRES); System.out.println("Audio sample in buffer length: " + audio.length); System.out.println("Filter length: " + filter.length); // designing the windowed sinc filter int cutFreq = 1000; for (int i = 0; i < filter.length-1; i++) { // see http://en.wikipedia.org/wiki/Sinc_filter double sincFilter = (2*cutFreq/(double)SAMPLERATE)*sinc(2*cutFreq*(i-((filter.length-1)/2.0))/(double)SAMPLERATE); // uncomment for a bandpass filter //sincFilter = sincFilter-(2*(cutFreq+1000)/(double)SAMPLERATE)*sinc(2*(cutFreq+1000)*(i-((filter.length-1)/2.0))/(double)SAMPLERATE); // uncomment for a highpass filter /*if (i != (filter.length-1)/2) sincFilter *= -1; else sincFilter = 1-sincFilter;*/ // applying a Hamming window, see http://stackoverflow.com/questions/5418951/what-is-the-hamming-window-for and http://en.wikipedia.org/wiki/Window_function //filter[i] = (0.53836 - (0.46164 * Math.cos((Math.PI*2) * (double)i / (double)(filter.length-1)))) * idealFilter; // applying a Hann window //filter[i] = 0.5*(1-Math.cos( (2*Math.PI*i)/(double)(filter.length-1) )) * sincFilter; // applying a Blackman window filter[i] = (0.42-0.5*Math.cos((2*Math.PI*i)/(double)(filter.length-1))+0.08*Math.cos((4*Math.PI*i)/(double)(filter.length-1))) * sincFilter; } // clearing the audio overlap buffer for (int i = 0; i < audioOverlap.length; i++) audioOverlap[i] = 0; // clearing the FFT buffer for (int i = 0; i < filterFFT.length; i++) filterFFT[i] = 0; // copying time domain filter data to the FFT buffer for (int i = 0; i < filter.length; i++) filterFFT[2 * i] = filter[i]; fft.complexForward(filterFFT); } private void lowPassFilter(double[] audioDataIn, double[] audioDataOut) { // zeroing out the audio FFT buffer for (int i = 0; i < audioFFT.length; i++) audioFFT[i] = 0; // copying audio data to the FFT data buffer for (int i = 0; i < audioDataIn.length; i++) audioFFT[2 * i] = audioDataIn[i]; // calculating the fft of the data fft.complexForward(audioFFT); // pointwise multiplication of the filter and audio data in the frequency domain for (int i = 0; i < filterFFT.length; i += 2) { double temp = audioFFT[i] * filterFFT[i] - audioFFT[i+1]*filterFFT[i+1]; audioFFT[i+1] = audioFFT[i] * filterFFT[i+1] + audioFFT[i+1] * filterFFT[i]; // imaginary part audioFFT[i] = temp; // real part } // built-in scaling hangs the thread, so we don't use it fft.complexInverse(audioFFT, false); // adding the first half of the audio FFT buffer to the overlap buffer for (int i = 0; i < audioDataOut.length; i++) audioDataOut[i] = (audioOverlap[i] + audioFFT[i * 2]) / 2000; // applying scaling // copying the second half of the audio FFT buffer to the audio overlap buffer for (int i = 0; i < audioOverlap.length; i++) audioOverlap[i] = audioFFT[audioFFT.length/2 + i * 2]; } @Override public void run() { tdl.start(); try { while (!Thread.interrupted()) { // waiting for the buffer to get filled while (tdl.available() < audioBytes.length) Thread.sleep(0, 1); // without this, the audio will be choppy int bytesRead = tdl.read(audioBytes, 0, audioBytes.length); // converting frames stored as bytes to double values int samplesRead = bytesRead / 2; for (int i = 0; i < samplesRead; i++) audio[i] = ((audioBytes[i * 2] & 0xFF) | (audioBytes[i * 2 + 1] << 8)) / 32768.0; lowPassFilter(audio, audioFiltered); baos.write(getBytesFromDoubles(audioFiltered, audioFiltered.length), 0, audioFiltered.length * 2); } } catch (InterruptedException e) { } tdl.stop(); tdl.close(); writeWavFile(baos.toByteArray(), baos.size() / 2, "output.wav"); } |
About me

I'm Nonoo. This is my blog about music, sounds, filmmaking, amateur radio, computers, programming, electronics and other things I'm obsessed with.
... »

 Projects
Projects


Hi,
Nice note about filtering signal in frequency domain. I’m only curious about one thing. Why scaling factor in:
audioDataOut[i] = (audioOverlap[i] + audioFFT[i * 2]) / 2000; // applying scaling
is exact 2000?
This is a value chosen empirically or I don’t understand something of this post and mentioned articles? :)
Greetings from Poland,
Michał
Hello, yes, this scaling value was chosen empirically :)
I am abit curious, how would this be applied with the overlap add, if what you were processing was realtime? like a function that has input and out as parameters? e.X: void process(double *input, double *output); which processed each sample? I tried myself, but i just can’t seem to get my head around it
Realtime processing of overlap add could be done on a buffer without problems.
Yeah probably, i’ve been sitting with this one for ages.
If i have a fft buffer which is based on a struct with two entries.
Im and Re. It makes sense to creata a buffer that is 1024 large. No need to think about multiplying i * 2 to get the real part, because i can simply just access the re or im with [i].re or [i].im in an iteration.
So anyhow, having two fft buffers, one filter and one with the signal.
You multiply them both, and the perform the inverse FFT on the multiplied result. This multiplied result should also be 1024 right?
In that case i dont see why and where you should introduce this overlap add in a realtime scenario.
Since here, i will have to wait until i have saved 1024 successful samples before i can begin to compute.
I guess this is not your problem what so ever, but i just can’t figure this out. It bothers me, i hate not being able to solve stuff :(
Thanks for writing this up, this far it’s been my only source of information about this.
iwant htis code in matlab could u please send it to me in my add ” [email protected]”
Sorry, I don’t have this code in Matlab.
I´m quite new in dsp world.
I have a little question about this line:
audio[i] = ((audioBytes[i * 2] & 0xFF) | (audioBytes[i * 2 + 1] << 8)) / 32768.0;
why do you divide by 32768?
Thanks for posting the code I was having big time trouble doing a low pass filter.
That line converts the 16 bit input value (stored as two bytes) to double (between 0 and 1).
Thanks.
Yes, but the max value of a 16-bit is 32767. The use of 32768.0 won’t cause any problems — you are simply decreasing the signal by 1/32768.
Hi
Thanks a lot for this!
I don’t know (don’t understand) how to set the bandwidth for the bandpass filter.
sincFilter-(2*(cutFreq+1000)/(double)SAMPLERATE)*sinc(2*(cutFreq+1000)*(i-((filter.length-1)/2.0))/(double)SAMPLERATE);
First I expected if going from cutFreq until cutFreq+1000, but it doesn’t seem to work like that…
Thanks in advance!
Sorry, my fault: Seems exactly to work like that …
Hi,
Thank you so much for this Tutorial, A really concise explanation. I have found simpler break downs of this process, for a DSP noob, very hard to find.
I have one question. I am trying to make a version of this to run in processing, due to my college assignment being implement a band pass filter in Processing.
Would you have any suggestions as to how I would need to change this into a processing version?
Thank you hugely as the step by step explanation has finaaly at least explained the full process to me in plain English!
Much appreciated
Hello! I’m happy that you’ve found these tutorials useful. Sadly I don’t know Processing. :(
Hi,
I found a site with dft filtering tutorial about a year ago, and
i cant seem to find it now, it had black background with green letters and some pictures of some robots drawing on paper, very interesting and fun to read. There was everything i needed for audio processing including all the math material complex numbers and stuff like that. So i was wandering if it was your website because your name (Nonoo) sounds very familiar to me?
Hello, it wasn’t my website. Maybe it was dspguide.com :)
It’s not dspguide.com, maybe the material is, but thanks anyway… :) although I really think it was your webpage, very good presentation;)
i am developing an Applicaton of speech Recognition using java. can someone help me to remove the background noise which comes
Hello,
Is there any way to calculate the scaling factor “2000” in order to get the original amplitude , based on cutoff frequency amplitude
is changing ?
Thanks
faltu