Single-sideband is one of the most popular modulation modes in analog voice radio communication today. SSB avoids the bandwidth doubling and unnecessary carrier emitting of amplitude modulation, thus concentrating radiated power only on the signal that carries the important information (for ex. voice).

If we take a 2KHz sine wave (modulator wave, this is the information we want to transport, so after demodulation, we would like to get this 2KHz beep) and modulate a 10KHz sine wave (carrier wave, this will carry our modulator wave) with it (you simply multiply the two sines), you get this:

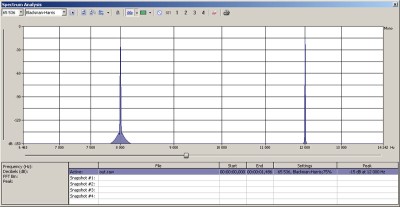
You can see the two sidebands: LSB – lower sideband, the 8KHz sine, USB – upper sideband, the 12KHz sine. If you do this 2 sine multiplication in analog electronics, you will also get the 10KHz carrier wave.

Now this means if you want to transmit this 2KHz sine wave over radio on (for example) 3.791MHz, in theory you multiply the 2KHz sine with a 3.791MHz sine and transmit that resulting signal. In this case you will have to transmit both sidebands – if you transmit with 100 watts, your output power will distribute between the two sidebands, so this is not good, you only want to transmit one of the sidebands with full power.

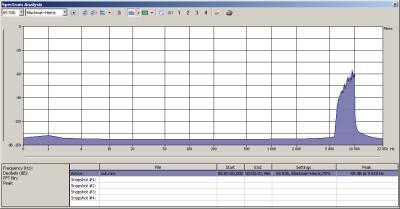
A 4KHz wide LSB modulated voice signal

I played with three methods of generating an SSB modulated signal in software.

The first method is a very straight approach and only can be realized in software with no real benefit: let’s multiply our modulator wave with the carrier and then lowpass (or highpass) the sideband we want to keep.

This needs very sharp filtering. In the example I used FFT on the output, zeroed out all the unnecessary bins and then made an inverse FFT and got the result.

Our buffer is exactly 44100 bytes long (this is the samplerate I used) and I set FFT_RES to this too, so the FFT library’s (libfftw) output is exactly linear, the 10000th bin means 10KHz and so on. In the example my carrier wave is a 10KHz sine, so I zeroed out all frequency components above that to get the lower sideband.

For demodulation of an SSB signal you can multiply it with a sine which has the frequency of the carrier wave (in this example 10KHz).

The second method is called the Hartley method. This method can be simulated very efficiently and easily in software. To generate an SSB signal with this method, two versions of the original signal are generated, mutually 90° out of phase. Each one of these signals is then mixed with carrier waves that are also 90° out of phase with each other. By either adding or subtracting the resulting signals, a lower or upper sideband signal results.

90 degrees phase delay can be realized with a Hilbert transformer. You can design one using this great page.

In this example I used a prerecorded voice with 4KHz bandwidth as the modulator. The carrier is at 10KHz. The resulting LSB signal can be seen here:

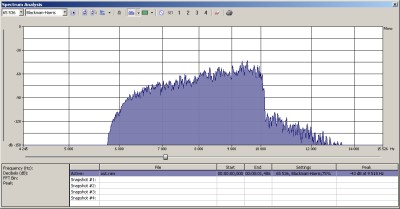
The third method is called the Weaver method. This is the most complicated one, it uses two quadrature oscillators and lowpass filters. A very nicely illustrated paper on this method can be downloaded here, read this if you want to learn the mechanisms of this method.

For lowpass filtering I used the previously described FFT – inverse FFT method.

The resulting signal:

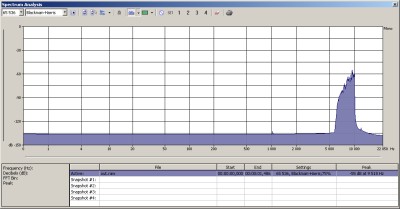
I hope you find this post useful. I had great time experimenting with all these stuff. More writings like this will come soon.